Asymptotes ng graph ng isang function
Ang multo ng asymptote ay gumagala sa site sa loob ng mahabang panahon upang sa wakas ay magkatotoo sa isang hiwalay na artikulo at magdala ng partikular na kasiyahan sa mga mambabasa na nalilito buong pag-aaral ng function. Ang paghahanap ng mga asymptotes ng isang graph ay isa sa ilang bahagi ng gawaing ito na saklaw sa kurso ng paaralan sa isang pangkalahatang-ideya na paraan, dahil ang mga kaganapan ay umiikot sa pagkalkula mga limitasyon sa pag-andar, ngunit nabibilang pa rin sila sa mas mataas na matematika. Para sa mga bisitang may kaunting pang-unawa sa mathematical analysis, sa tingin ko ay malinaw ang pahiwatig ;-) ...stop, stop, saan ka pupunta? Mga limitasyon- madali lang!
Ang mga halimbawa ng asymptotes ay nakatagpo kaagad sa unang aralin tungkol sa mga graph ng elementarya function, at ang paksa ay tumatanggap na ngayon ng detalyadong pagsasaalang-alang.
Kaya ano ang isang asymptote?
Imagine variable na punto, na "naglalakbay" kasama ang graph ng function. Asymptote ay tuwid, sa whcih malapit nang walang katapusan ang graph ng isang function ay lumalapit habang ang variable point nito ay gumagalaw sa infinity.
Tandaan : Ang kahulugan ay makabuluhan, kung kailangan mo ng pormulasyon sa calculus notation, mangyaring sumangguni sa aklat-aralin.
Sa eroplano, ang mga asymptote ay inuri ayon sa kanilang natural na lokasyon:
1) Mga patayong asymptotes, na ibinibigay ng isang equation ng form , kung saan ang "alpha" ay isang tunay na numero. Tinutukoy ng isang sikat na kinatawan ang ordinate axis mismo,
na may bahagyang pakiramdam ng pagduduwal naaalala natin ang hyperbole.
2) Oblique asymptotes tradisyonal na nakasulat equation ng isang tuwid na linya na may isang angle coefficient. Minsan ang isang espesyal na kaso ay kinilala bilang isang hiwalay na grupo - pahalang na asymptotes. Halimbawa, ang parehong hyperbola na may asymptote.
Bilisan natin, pindutin natin ang paksa sa isang maikling putok ng machine gun:
Ilang asymptotes ang maaaring mayroon ang graph ng isang function?
Hindi isa, isa, dalawa, tatlo,... o walang katapusang marami. Hindi tayo lalayo para sa mga halimbawa, tandaan natin mga pag-andar ng elementarya. Ang isang parabola, isang cubic parabola, at isang sine wave ay walang mga asymptotes. Ang graph ng isang exponential, logarithmic function ay may isang solong asymptote. Ang arctangent at arccotangent ay may dalawa sa kanila, at ang tangent at cotangent ay may walang katapusang marami. Karaniwan para sa isang graph na magkaroon ng parehong pahalang at patayong mga asymptotes. Hyperbole, mamahalin ka palagi.
Ano ang ibig sabihin?
Vertical asymptotes ng graph ng isang function
Karaniwang matatagpuan ang patayong asymptote ng graph sa punto ng walang katapusang discontinuity mga function. Ito ay simple: kung sa isang punto ang function ay dumaranas ng isang walang katapusang discontinuity, kung gayon ang tuwid na linya na tinukoy ng equation ay ang vertical asymptote ng graph.
Tandaan : Tandaan na ang entry ay ginagamit upang sumangguni sa dalawang ganap na magkaibang konsepto. Kung ang isang punto ay ipinahiwatig o isang equation ng isang linya ay nakasalalay sa konteksto.
Kaya, upang maitaguyod ang pagkakaroon ng isang patayong asymptote sa isang punto, sapat na upang ipakita iyon kahit isa mula sa isang panig na mga limitasyon 
walang hanggan. Kadalasan ito ang punto kung saan ang denominator ng function ay zero. Sa esensya, nakakita na kami ng mga patayong asymptote sa mga huling halimbawa ng aralin sa pagpapatuloy ng isang function. Ngunit sa ilang mga kaso mayroon lamang isang panig na limitasyon, at kung ito ay walang katapusan, pagkatapos ay muli - mahalin at pabor sa vertical asymptote. Ang pinakasimpleng paglalarawan: at ang ordinate axis (tingnan. Mga graph at katangian ng elementarya na pag-andar).
Mula sa itaas, ang isang malinaw na katotohanan ay sumusunod din: kung tuluy-tuloy ang function, pagkatapos ay walang mga patayong asymptotes. Sa ilang kadahilanan, isang parabola ang naisip. Talaga, saan ka maaaring "magdikit" ng isang tuwid na linya dito? ...oo... naiintindihan ko... Nag hysterical ang followers ni Uncle Freud =)
Ang kabaligtaran na pahayag ay karaniwang mali: halimbawa, ang function ay hindi tinukoy sa buong linya ng numero, ngunit ganap na pinagkaitan ng mga asymptotes.
Mga sloping asymptotes ng graph ng isang function
Ang mga oblique (bilang isang espesyal na kaso - pahalang) asymptotes ay maaaring iguhit kung ang argumento ng function ay may posibilidad na "plus infinity" o sa "minus infinity". kaya lang ang graph ng isang function ay hindi maaaring magkaroon ng higit sa dalawang slanting asymptotes. Halimbawa, ang graph ng isang exponential function ay may isang pahalang na asymptote sa , at ang graph ng arctangent at ay may dalawang ganoong asymptotes, at magkaiba ang mga iyon.
Kapag ang graph sa parehong mga lugar ay lumalapit sa isang pahilig na asymptote, ang "infinities" ay karaniwang pinagsama sa ilalim ng isang entry. Halimbawa, ...tama ang nahulaan mo: .
Pangkalahatang tuntunin ng hinlalaki:
Kung may dalawa pangwakas limitasyon 
, pagkatapos ay ang tuwid na linya ay ang pahilig na asymptote ng graph ng function sa . Kung kahit isa ng mga nakalistang limitasyon ay walang hanggan, pagkatapos ay walang pahilig na asymptote.
Tandaan : ang mga formula ay mananatiling wasto kung ang "x" ay may posibilidad na "plus infinity" o "minus infinity" lamang.
Ipakita natin na ang parabola ay walang oblique asymptotes: 
Ang limitasyon ay walang hanggan, na nangangahulugang walang oblique asymptote. Tandaan na sa paghahanap ng limitasyon 
nawala ang pangangailangan dahil natanggap na ang sagot.
Tandaan
: Kung mayroon kang (o magkakaroon) ng mga kahirapan sa pag-unawa sa plus-minus, minus-plus sign, mangyaring tingnan ang tulong sa simula ng aralin
sa infinitesimal functions, kung saan sinabi ko sa iyo kung paano wastong bigyang-kahulugan ang mga palatandaang ito.
Malinaw na ang anumang quadratic, cubic function, polynomial ng ika-4 at mas mataas na degree ay wala ring oblique asymptotes.
Ngayon, tiyakin natin na ang graph ay wala ring oblique asymptote. Upang ipakita ang kawalan ng katiyakan na ginagamit namin Ang panuntunan ng L'Hopital:
, na kung ano ang kailangang suriin.
Kapag ang function ay lumalaki nang walang katiyakan, ngunit walang tuwid na linya kung saan lalapit ang graph nito walang katapusang malapit.
Lumipat tayo sa praktikal na bahagi ng aralin:
Paano mahahanap ang mga asymptotes ng graph ng isang function?
Ito ay eksakto kung paano ang karaniwang gawain ay nabuo, at ito ay nagsasangkot ng paghahanap ng LAHAT ng mga asymptotes ng graph (vertical, inclined/horizontal). Bagaman, upang maging mas tumpak sa paglalagay ng tanong, pinag-uusapan natin ang tungkol sa pananaliksik para sa pagkakaroon ng mga asymptotes (pagkatapos ng lahat, maaaring wala man lang). Magsimula tayo sa isang simpleng bagay:
Halimbawa 1
Maghanap ng mga asymptotes ng graph ng isang function
Solusyon Maginhawang hatiin ito sa dalawang punto:
1) Una naming suriin kung mayroong mga vertical asymptotes. Ang denominator ay napupunta sa zero sa , at agad na malinaw na sa puntong ito ang function ay naghihirap walang katapusang agwat, at ang tuwid na linya na ibinigay ng equation ay ang patayong asymptote ng graph ng function. Ngunit, bago gumuhit ng gayong konklusyon, kinakailangan upang makahanap ng isang panig na mga limitasyon: 
Ipinaaalaala ko sa iyo ang pamamaraan ng pagkalkula na katulad ko na nakatuon sa artikulo Pagpapatuloy ng pag-andar. Mga break point. Sa expression sa ilalim ng limit sign pinapalitan namin . Walang kawili-wili sa numerator:
.
Pero sa denominator pala infinitesimal na negatibong numero:
, tinutukoy nito ang kapalaran ng limitasyon.
Ang limitasyon sa kaliwang kamay ay walang hanggan, at, sa prinsipyo, posible nang gumawa ng hatol tungkol sa pagkakaroon ng isang patayong asymptote. Ngunit ang mga unilateral na limitasyon ay kailangan hindi lamang para dito - TUMULONG SA PAG-UNAWA PAANO hanapin ang graph ng function at buuin ito TAMA. Samakatuwid, dapat din nating kalkulahin ang limitasyon sa kanang kamay: 
Konklusyon: walang hanggan ang mga one-sided na limitasyon, na nangangahulugan na ang tuwid na linya ay ang patayong asymptote ng graph ng function sa .
Unang limitasyon may hangganan, na nangangahulugang kinakailangan na "ipagpatuloy ang pag-uusap" at hanapin ang pangalawang limitasyon:
Ang pangalawang limitasyon din may hangganan.
Kaya, ang aming asymptote ay:
Konklusyon: ang tuwid na linya na ibinigay ng equation ay ang pahalang na asymptote ng graph ng function sa .
Upang mahanap ang pahalang na asymptote
maaari kang gumamit ng pinasimpleng formula:
Kung meron may hangganan limitasyon, kung gayon ang tuwid na linya ay ang pahalang na asymptote ng graph ng function sa .
Madaling makita na ang numerator at denominator ng function parehong pagkakasunud-sunod ng paglago, na nangangahulugang ang hinahanap na limitasyon ay magiging may hangganan: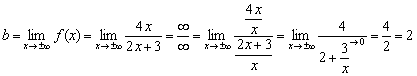 
Sagot:
Ayon sa kondisyon, hindi mo kailangang kumpletuhin ang pagguhit, ngunit kung puspusan pag-aaral ng function, pagkatapos ay sa draft agad kaming gumawa ng sketch: 
Batay sa tatlong nahanap na limitasyon, subukang alamin para sa iyong sarili kung paano matatagpuan ang graph ng function. Mahirap ba talaga? Maghanap ng 5-6-7-8 puntos at markahan ang mga ito sa guhit. Gayunpaman, ang graph ng function na ito ay binuo gamit ang pagbabago ng graph ng isang elementary function, at ang mga mambabasa na maingat na nagsuri sa Halimbawa 21 ng artikulo sa itaas ay madaling mahulaan kung anong uri ito ng kurba.
Halimbawa 2
Maghanap ng mga asymptotes ng graph ng isang function
Ito ay isang halimbawa para malutas mo nang mag-isa. Hayaan akong ipaalala sa iyo na ito ay maginhawa upang hatiin ang proseso sa dalawang punto - vertical asymptotes at oblique asymptotes. Sa sample na solusyon, ang pahalang na asymptote ay matatagpuan gamit ang isang pinasimple na pamamaraan.
Sa pagsasagawa, ang mga fractional-rational function ay madalas na nakatagpo, at pagkatapos ng pagsasanay sa hyperbolas, gagawin naming kumplikado ang gawain:
Halimbawa 3
Maghanap ng mga asymptotes ng graph ng isang function 
Solusyon: Isa, dalawa at tapos na:
1) Matatagpuan ang mga patayong asymptote sa mga punto ng walang katapusang discontinuity, kaya kailangan mong suriin kung ang denominator ay napupunta sa zero. Magdesisyon tayo quadratic equation:
Ang discriminant ay positibo, kaya ang equation ay may dalawang tunay na ugat, at ang trabaho ay tumaas nang malaki =) 
Upang higit pang makahanap ng isang panig na mga limitasyon, ito ay maginhawa upang i-factorize ang square trinomial:
(para sa compact notation, ang "minus" ay kasama sa unang bracket). Upang maging ligtas, suriin natin sa pamamagitan ng pagbubukas ng mga bracket sa isip o sa isang draft.
Isulat muli natin ang function sa form 
Maghanap tayo ng isang panig na limitasyon sa puntong ito: 
At sa puntong: 
Kaya, ang mga tuwid na linya ay mga patayong asymptotes ng graph ng function na pinag-uusapan.
2) Kung titingnan mo ang function 
, pagkatapos ay medyo halata na ang limitasyon ay magiging may hangganan at mayroon kaming pahalang na asymptote. Ipakita natin ang presensya nito sa maikling paraan: 
Kaya, ang tuwid na linya (abscissa axis) ay ang pahalang na asymptote ng graph ng function na ito.
Sagot:
Ang mga nahanap na limitasyon at asymptotes ay nagbibigay ng maraming impormasyon tungkol sa graph ng function. Subukang isipin ang pagguhit na isinasaalang-alang ang mga sumusunod na katotohanan: 
I-sketch ang iyong bersyon ng graph sa iyong draft.
Siyempre, hindi malinaw na tinutukoy ng mga limitasyon na natagpuan ang hitsura ng graph, at maaari kang magkamali, ngunit ang ehersisyo mismo ay magbibigay ng napakahalagang tulong sa panahon ng full function study. Ang tamang larawan ay nasa katapusan ng aralin.
Halimbawa 4
Maghanap ng mga asymptotes ng graph ng isang function
Halimbawa 5
Maghanap ng mga asymptotes ng graph ng isang function 
Ito ay mga gawain para sa independiyenteng solusyon. Ang parehong mga graph ay muling may mga pahalang na asymptote, na agad na natukoy ng mga sumusunod na tampok: sa Halimbawa 4 kaayusan ng paglago denominador higit pa, kaysa sa pagkakasunud-sunod ng paglago ng numerator, at sa Halimbawa 5 ang numerator at denominator parehong pagkakasunud-sunod ng paglago. Sa sample na solusyon, ang unang function ay sinusuri para sa pagkakaroon ng mga pahilig na asymptotes nang buo, at ang pangalawa - sa pamamagitan ng limitasyon.
Ang mga pahalang na asymptote, sa aking pansariling impresyon, ay kapansin-pansing mas karaniwan kaysa sa mga "tunay na nakatagilid." Ang pinakahihintay na pangkalahatang kaso:
Halimbawa 6
Maghanap ng mga asymptotes ng graph ng isang function 
Solusyon: mga klasiko ng genre:
1) Dahil ang denominator ay positibo, pagkatapos ay ang function tuloy-tuloy kasama ang buong linya ng numero, at walang mga patayong asymptotes. …Maganda ba? Hindi ang tamang salita - mahusay! Ang Point No. 1 ay sarado.
2) Suriin natin ang pagkakaroon ng mga pahilig na asymptotes:
Unang limitasyon may hangganan, kaya magpatuloy tayo. Sa panahon ng pagkalkula ng pangalawang limitasyon upang maalis kawalan ng katiyakan "infinity minus infinity" Dinadala namin ang expression sa isang karaniwang denominator: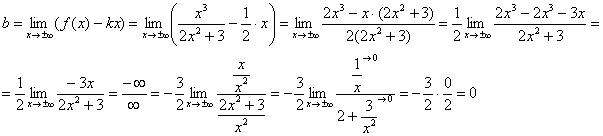 
Ang pangalawang limitasyon din may hangganan Samakatuwid, ang graph ng function na pinag-uusapan ay may oblique asymptote:
Konklusyon:
Kaya, kapag ang graph ng function 
walang katapusang malapit lumalapit sa isang tuwid na linya: 
Tandaan na ito ay sumasalubong sa pahilig na asymptote nito sa pinanggalingan, at ang mga naturang intersection point ay lubos na katanggap-tanggap - mahalaga na "ang lahat ay normal" sa kawalang-hanggan (sa katunayan, ito ay kung saan pinag-uusapan natin ang tungkol sa mga asymptotes).
Halimbawa 7
Maghanap ng mga asymptotes ng graph ng isang function
Solusyon: Walang espesyal na komento, kaya gagawa ako ng tinatayang halimbawa ng malinis na solusyon:
1) Mga patayong asymptotes. Tuklasin natin ang punto. 
Ang tuwid na linya ay ang patayong asymptote para sa graph sa .
2) Oblique asymptotes: 
Ang tuwid na linya ay ang slanted asymptote para sa graph sa .
Sagot: 
Ang mga nakitang one-sided na limitasyon at asymptotes ay nagbibigay-daan sa amin na mahulaan nang may mataas na kumpiyansa kung ano ang hitsura ng graph ng function na ito. Tamang pagguhit sa pagtatapos ng aralin.
Halimbawa 8
Maghanap ng mga asymptotes ng graph ng isang function
Ito ay isang halimbawa para sa independiyenteng solusyon; para sa kaginhawahan ng pagkalkula ng ilang mga limitasyon, maaari mong hatiin ang numerator sa pamamagitan ng termino ng denominator ayon sa termino. Muli, kapag sinusuri ang iyong mga resulta, subukang gumuhit ng graph ng function na ito.
Malinaw, ang mga may-ari ng "totoong" oblique asymptotes ay ang mga graph ng mga fractional rational function na ang pinakamataas na antas ng numerator. isa pa ang pinakamataas na antas ng denominator. Kung ito ay higit pa, hindi magkakaroon ng oblique asymptote (halimbawa, ).
Ngunit ang iba pang mga himala ay nangyayari sa buhay:
Halimbawa 9
Halimbawa 11
Suriin ang graph ng isang function para sa pagkakaroon ng mga asymptotes
Solusyon: halata naman eh 
, samakatuwid ay isinasaalang-alang lamang namin ang tamang kalahating eroplano, kung saan mayroong isang graph ng function.
Kaya, ang tuwid na linya (ordinate axis) ay ang patayong asymptote para sa graph ng function sa .
2) Ang pag-aaral sa oblique asymptote ay maaaring isagawa ayon sa buong pamamaraan, ngunit sa artikulo Mga patakaran ng L'Hopital nalaman namin na ang isang linear function ay may mas mataas na pagkakasunud-sunod ng paglago kaysa sa isang logarithmic, samakatuwid: 
(Tingnan ang Halimbawa 1 ng parehong aralin).
Konklusyon: ang x-axis ay ang pahalang na asymptote ng graph ng function sa .
Sagot:
, Kung ;
, Kung .
Pagguhit para sa kalinawan: 
Ito ay kagiliw-giliw na ang isang tila katulad na pag-andar ay walang mga asymptotes sa lahat (maaaring suriin ito ng mga nais).
Dalawang huling halimbawa para sa sariling pag-aaral:
Halimbawa 12
Suriin ang graph ng isang function para sa pagkakaroon ng mga asymptotes 
Asymptote ng graph ng isang function Ang y = f(x) ay isang tuwid na linya na may katangian na ang distansya mula sa punto (x, f(x)) hanggang sa tuwid na linyang ito ay nagiging zero habang ang graph point ay gumagalaw nang walang katiyakan mula sa pinanggalingan.
Sa Figure 3.10. Ang mga graphic na halimbawa ay ibinigay patayo, pahalang At hilig asymptote.
Ang paghahanap ng mga asymptotes ng graph ay batay sa sumusunod na tatlong theorems.
Vertical asymptote theorem. Hayaang tukuyin ang function na y = f(x) sa isang tiyak na kapitbahayan ng punto x 0 (maaaring hindi kasama ang puntong ito mismo) at hindi bababa sa isa sa mga one-sided na limitasyon ng function ay katumbas ng infinity, i.e. Pagkatapos ang tuwid na linyang x = x 0 ay ang patayong asymptote ng graph ng function na y = f(x).
Malinaw, ang tuwid na linya x = x 0 ay hindi maaaring maging isang patayong asymptote kung ang function ay tuloy-tuloy sa puntong x 0, dahil sa kasong ito 
. Dahil dito, dapat hanapin ang mga vertical asymptotes sa mga discontinuity point ng function o sa mga dulo ng domain of definition nito.
Pahalang na asymptote theorem. Hayaang tukuyin ang function na y = f(x) para sa sapat na malaking x at may hangganan na limitasyon ng function. Pagkatapos ang linyang y = b ay ang pahalang na asymptote ng graph ng function.
Magkomento. Kung ang isa lamang sa mga limitasyon ay may hangganan, kung gayon ang pag-andar ay may, nang naaayon, kaliwete o kanang bahagi pahalang na asymptote.
Kung sakaling ang , ang function ay maaaring magkaroon ng oblique asymptote.
Oblique asymptote theorem. Hayaang tukuyin ang function na y = f(x) para sa sapat na malaking x at may mga limitasyon 
. Pagkatapos ang tuwid na linya na y = kx + b ay ang slanted asymptote ng graph ng function.
Walang patunay.
Ang isang pahilig na asymptote, tulad ng isang pahalang, ay maaaring maging kanan o kaliwang kamay kung ang batayan ng kaukulang mga limitasyon ay infinity ng isang tiyak na tanda.
Ang pag-aaral ng mga function at pagbuo ng kanilang mga graph ay karaniwang kinabibilangan ng mga sumusunod na hakbang:
1. Hanapin ang domain ng kahulugan ng function.
2. Suriin ang function para sa even-odd parity.
3. Maghanap ng mga vertical na asymptotes sa pamamagitan ng pagsusuri sa mga discontinuity point at ang pag-uugali ng function sa mga hangganan ng domain ng kahulugan, kung ang mga ito ay may hangganan.
4. Maghanap ng mga pahalang o pahilig na asymptotes sa pamamagitan ng pagsusuri sa gawi ng function sa infinity.
5. Maghanap ng extrema at mga pagitan ng monotonicity ng function.
6. Hanapin ang mga pagitan ng convexity ng function at inflection point.
7. Hanapin ang mga punto ng intersection sa mga coordinate axes at, posibleng, ilang karagdagang mga punto na nagpapalinaw sa graph.
Pagkakaiba ng pag-andar
Mapapatunayan na kung ang isang function ay may limitasyon na katumbas ng isang may hangganang numero para sa isang tiyak na base, maaari itong irepresenta bilang kabuuan ng numerong ito at isang infinitesimal na halaga para sa parehong base (at kabaliktaran): .
Ilapat natin ang theorem na ito sa isang differentiable function: .
Kaya, ang pagtaas ng function na Dу ay binubuo ng dalawang termino: 1) linear na may paggalang sa Dх, i.e. f `(x)Dх; 2) nonlinear na may paggalang sa Dx, ibig sabihin. a(Dx)Dх. Kasabay nito, mula noon 
, ang pangalawang terminong ito ay isang infinitesimal ng isang mas mataas na pagkakasunud-sunod kaysa sa Dx (dahil ang Dx ay may posibilidad na zero, ito ay may posibilidad na maging zero kahit na mas mabilis).
Differential Ang function ay ang pangunahing, linear na may kaugnayan sa Dx na bahagi ng pagtaas ng function, katumbas ng produkto ng derivative at ang pagtaas ng independent variable na dy = f `(x)Dx.
Hanapin natin ang kaugalian ng function na y = x.
Dahil dy = f `(x)Dх = x`Dх = Dх, pagkatapos ay dx = Dх, i.e. ang differential ng isang independent variable ay katumbas ng increment ng variable na ito.
Samakatuwid, ang formula para sa kaugalian ng isang function ay maaaring isulat bilang dy = f `(x)dх. Kaya naman ang isa sa mga notasyon para sa derivative ay ang fraction na dy/dх.
Ang geometric na kahulugan ng kaugalian ay inilalarawan
Larawan 3.11. Kumuha tayo ng di-makatwirang punto M(x, y) sa graph ng function na y = f(x). Bigyan natin ang argumentong x ng increment na Dx. Pagkatapos ang function na y = f(x) ay tatanggap ng increment Dy = f(x + Dх) - f(x). Gumuhit tayo ng tangent sa graph ng function sa point M, na bumubuo ng isang anggulo a na may positibong direksyon ng abscissa axis, i.e. f `(x) = kayumanggi a. Mula sa kanang tatsulok MKN
KN = MN*tg a = Dх*tg a = f `(x)Dх = dy.
Kaya, ang differential ng isang function ay ang pagtaas sa ordinate ng tangent na iginuhit sa graph ng function sa isang naibigay na punto kapag natanggap ng x ang increment na Dx.
Ang mga katangian ng isang kaugalian ay karaniwang pareho sa mga katangian ng isang derivative:
3. d(u ± v) = du ± dv.
4. d(uv) = v du + u dv.
5. d(u/v) = (v du - u dv)/v 2.
Gayunpaman, mayroong isang mahalagang pag-aari ng kaugalian ng isang function na wala ang derivative nito - ito ay invariance ng differential form.
Mula sa kahulugan ng differential para sa function na y = f(x), ang differential dy = f `(x)dх. Kung ang function na ito y ay kumplikado, i.e. y = f(u), kung saan u = j(x), pagkatapos ay y = f at f `(x) = f `(u)*u`. Pagkatapos dy = f `(u)*u`dх. Ngunit para sa pag-andar
u = j(x) differential du = u`dх. Kaya dy = f `(u)*du.
Paghahambing ng mga pagkakapantay-pantay na dy = f `(x)dх at dy = f `(u)*du, tinitiyak namin na hindi magbabago ang differential formula kung sa halip na isang function ng independent variable x ay isasaalang-alang namin ang isang function ng dependent variable u. Ang katangiang ito ng isang kaugalian ay tinatawag na invariance (i.e., immutability) ng anyo (o formula) ng differential.
Gayunpaman, mayroon pa ring pagkakaiba sa dalawang formula na ito: sa una sa kanila, ang pagkakaiba ng independent variable ay katumbas ng pagtaas ng variable na ito, i.e. dx = Dx, at pangalawa, ang pagkakaiba ng function na du ay ang linear na bahagi lamang ng pagtaas ng function na ito Du at para lamang sa maliit na Dx du » Du.
Ang solusyon ay maaaring maginhawang nahahati sa dalawang punto:
1) Una naming suriin kung mayroong mga vertical asymptotes. Ang denominator ay napupunta sa zero sa, at agad na malinaw na sa puntong ito ang function ay nagdurusa ng isang walang katapusang discontinuity, at ang tuwid na linya na tinukoy ng equation ay ang vertical asymptote ng graph ng function. Ngunit, bago gumuhit ng gayong konklusyon, kinakailangan upang makahanap ng isang panig na mga limitasyon:
Ipinapaalala ko sa iyo ang pamamaraan ng pagkalkula na katulad kong pinagtuunan ng pansin sa artikulong Continuity ng isang function. Mga breaking points. Pinapalitan namin ang "X" sa expression sa ilalim ng sign ng limitasyon. Walang kawili-wili sa numerator:
Ngunit ang denominator ay nagreresulta sa isang napakaliit na negatibong numero:
Tinutukoy nito ang kapalaran ng limitasyon.
Ang limitasyon sa kaliwang kamay ay walang hanggan, at, sa prinsipyo, posible nang gumawa ng hatol tungkol sa pagkakaroon ng isang patayong asymptote. Ngunit kailangan ang mga one-sided na limitasyon hindi lamang para dito - TUMULONG ang mga ito upang MAUNAWAAN KUNG PAANO matatagpuan ang graph ng isang function at upang maibuo ito nang TAMA. Samakatuwid, dapat din nating kalkulahin ang limitasyon sa kanang kamay:
Konklusyon: ang mga one-sided na limitasyon ay walang katapusan, na nangangahulugang ang tuwid na linya ay ang patayong asymptote ng graph ng function sa.
Ang unang limitasyon ay may hangganan, na nangangahulugang kailangan nating "ipagpatuloy ang pag-uusap" at hanapin ang pangalawang limitasyon:
Ang pangalawang limitasyon ay may hangganan din.
Kaya, ang aming asymptote ay:
Konklusyon: ang tuwid na linya na tinukoy ng equation ay ang pahalang na asymptote ng graph ng function sa.
Upang mahanap ang pahalang na asymptote, maaari kang gumamit ng pinasimpleng formula:
Kung may hangganan ang limitasyon, ang tuwid na linya ay ang pahalang na asymptote ng graph ng function sa.
Madaling mapansin na ang numerator at denominator ng function ay nasa parehong pagkakasunud-sunod ng paglago, na nangangahulugan na ang hinahanap na limitasyon ay magiging may hangganan:
Ayon sa kondisyon, hindi na kailangang gumawa ng isang pagguhit, ngunit kung tayo ay nasa gitna ng pagsasaliksik ng isang function, pagkatapos ay agad kaming gumawa ng isang sketch sa draft:
Batay sa tatlong limitasyon na natagpuan, subukang alamin para sa iyong sarili kung paano matatagpuan ang graph ng function. Mahirap ba talaga? Maghanap ng 5-6-7-8 puntos at markahan ang mga ito sa guhit. Gayunpaman, ang graph ng function na ito ay binuo gamit ang mga transformation ng graph ng isang elementary function, at ang mga mambabasa na maingat na nagsuri sa Halimbawa 21 ng artikulong ito ay madaling mahulaan kung anong uri ng curve ito.
Ito ay isang halimbawa para malutas mo nang mag-isa. Hayaan akong ipaalala sa iyo na ang proseso ay maginhawang nahahati sa dalawang punto - vertical asymptotes at oblique asymptotes. Sa sample na solusyon, ang pahalang na asymptote ay matatagpuan gamit ang isang pinasimple na pamamaraan.
Sa pagsasagawa, ang mga fractional-rational function ay madalas na nakatagpo, at pagkatapos ng pagsasanay sa hyperbolas, gagawin naming kumplikado ang gawain:
Maghanap ng mga asymptotes ng graph ng isang function
Solusyon: Isa, dalawa at tapos na:
1) Ang mga vertical na asymptote ay nasa mga punto ng walang katapusang discontinuity, kaya kailangan mong suriin kung ang denominator ay napupunta sa zero. Lutasin natin ang quadratic equation:
Ang discriminant ay positibo, kaya ang equation ay may dalawang tunay na ugat, at ang gawain ay idinagdag nang malaki
Upang higit pang makahanap ng isang panig na mga limitasyon, maginhawang i-factorize ang square trinomial:
(para sa compact notation, ang "minus" ay kasama sa unang bracket). Upang maging ligtas, suriin natin sa pamamagitan ng pagbubukas ng mga bracket sa isip o sa isang draft.
Isulat muli natin ang function sa form
Maghanap tayo ng isang panig na limitasyon sa puntong ito:
asymptote graph function na limitasyon
At sa puntong:
Kaya, ang mga tuwid na linya ay mga patayong asymptotes ng graph ng function na pinag-uusapan.
2) Kung titingnan mo ang function, medyo halata na ang limitasyon ay magiging may hangganan at mayroon kaming horizontal asymptote. Ipakita natin ang presensya nito sa maikling paraan:
Kaya, ang tuwid na linya (abscissa axis) ay ang pahalang na asymptote ng graph ng function na ito.
Ang mga nahanap na limitasyon at asymptotes ay nagbibigay ng maraming impormasyon tungkol sa graph ng function. Subukang isipin ang pagguhit na isinasaalang-alang ang mga sumusunod na katotohanan:
I-sketch ang iyong bersyon ng graph sa iyong draft.
Siyempre, hindi malinaw na tinutukoy ng mga nahanap na limitasyon ang hitsura ng graph, at maaari kang magkamali, ngunit ang ehersisyo mismo ay magbibigay ng napakahalagang tulong sa kurso ng isang kumpletong pag-aaral ng function. Ang tamang larawan ay nasa katapusan ng aralin.
Maghanap ng mga asymptotes ng graph ng isang function
Maghanap ng mga asymptotes ng graph ng isang function
Ito ay mga gawain para sa independiyenteng solusyon. Ang parehong mga graph ay may mga pahalang na asymptotes, na agad na nakita ng mga sumusunod na tampok: sa Halimbawa 4, ang pagkakasunud-sunod ng paglago ng denominator ay mas malaki kaysa sa pagkakasunud-sunod ng paglago ng numerator, at sa Halimbawa 5, ang numerator at denominator ay sa parehong pagkakasunud-sunod ng paglago. Sa sample na solusyon, ang unang function ay sinusuri para sa pagkakaroon ng mga pahilig na asymptotes nang buo, at ang pangalawa - sa pamamagitan ng limitasyon.
Ang mga pahalang na asymptote, sa aking pansariling impresyon, ay kapansin-pansing mas karaniwan kaysa sa mga "tunay na nakatagilid." Ang pinakahihintay na pangkalahatang kaso:
Maghanap ng mga asymptotes ng graph ng isang function
Solusyon: klasiko ng genre:
- 1) Dahil ang denominator ay positibo, ang function ay tuloy-tuloy sa buong linya ng numero, at walang mga patayong asymptotes. …Maganda ba? Hindi ang tamang salita - mahusay! Ang Point No. 1 ay sarado.
- 2) Suriin natin ang pagkakaroon ng mga pahilig na asymptotes:
Ang pangalawang limitasyon ay may hangganan din, samakatuwid, ang graph ng pinag-uusapang function ay may pahilig na asymptote:
Kaya, kapag ang graph ng function ay lumalapit sa isang tuwid na linya na walang katapusan na malapit.
Tandaan na ito ay sumasalubong sa pahilig na asymptote nito sa pinanggalingan, at ang mga naturang intersection point ay lubos na katanggap-tanggap - mahalaga na "ang lahat ay normal" sa kawalang-hanggan (sa katunayan, ito ay kung saan pinag-uusapan natin ang tungkol sa mga asymptotes).
Maghanap ng mga asymptotes ng graph ng isang function
Solusyon: walang espesyal na komento, kaya gagawa ako ng tinatayang halimbawa ng panghuling solusyon:
1) Mga patayong asymptotes. Tuklasin natin ang punto.
Ang tuwid na linya ay ang patayong asymptote para sa graph sa.
2) Oblique asymptotes:
Ang tuwid na linya ay ang slanted asymptote para sa graph sa.
Ang mga nakitang one-sided na limitasyon at asymptotes ay nagbibigay-daan sa amin na mahulaan nang may mataas na kumpiyansa kung ano ang hitsura ng graph ng function na ito.
Maghanap ng mga asymptotes ng graph ng isang function
Ito ay isang halimbawa para sa independiyenteng solusyon; para sa kaginhawahan ng pagkalkula ng ilang mga limitasyon, maaari mong hatiin ang numerator sa pamamagitan ng termino ng denominator ayon sa termino. Muli, kapag sinusuri ang iyong mga resulta, subukang gumuhit ng graph ng function na ito.
Malinaw, ang mga may-ari ng "tunay" na oblique asymptotes ay ang mga graph ng mga fractional rational function na kung saan ang nangungunang antas ng numerator ay isa na mas mataas kaysa sa nangungunang antas ng denominator. Kung ito ay higit pa, hindi na magkakaroon ng oblique asymptote (halimbawa).
Ngunit iba pang mga himala ang nangyayari sa buhay.
- Ang konsepto ng asymptotes
Ang isa sa mahahalagang yugto ng pagbuo ng mga function graph ay ang paghahanap ng mga asymptotes. Nakatagpo kami ng mga asymptotes nang higit sa isang beses: kapag gumagawa ng mga graph ng mga function, y=tgx, y=сtgx. Tinukoy namin ang mga ito bilang mga linya kung saan "may posibilidad" ang graph ng isang function, ngunit hindi kailanman tumatawid. Dumating na ang oras upang magbigay ng tumpak na kahulugan ng mga asymptotes.
May tatlong uri ng asymptotes: patayo, pahalang at pahilig. Sa pagguhit, ang mga asymptote ay karaniwang tinutukoy ng mga tuldok na linya.
Isaalang-alang natin ang sumusunod na artipisyal na binuong graph ng function (Larawan 16.1), isang halimbawa kung saan ipinapakita ang lahat ng uri ng asymptotes:
Tukuyin natin ang bawat uri ng asymptote:
1. Direkta x=a tinawag patayong asymptote function kung .
2. Direkta y=c tinawag pahalang na asymptote function kung .
3. Direkta y=kx+b tinawag pahilig na asymptote function kung .
Sa geometriko, ang kahulugan ng isang pahilig na asymptote ay nangangahulugan na sa →∞ ang graph ng function ay lumalapit sa isang tuwid na linya na malapit sa gusto y=kx+b, ibig sabihin. halos magkapareho sila. Ang pagkakaiba sa pagitan ng halos magkaparehong mga expression ay may posibilidad na zero.
Tandaan na ang mga pahalang at pahilig na asymptote ay isinasaalang-alang lamang sa ilalim ng kundisyong →∞. Minsan sila ay nakikilala sa pahalang at pahilig na mga asymptotes sa →+∞ at →-∞.
- Algorithm para sa paghahanap ng mga asymptotes
Upang makahanap ng mga asymptotes, maaari mong gamitin ang sumusunod na algorithm:
Maaaring may isa, marami o walang vertical asymptotes.
- Kung ang c ay isang numero, kung gayon y=c- pahalang na asymptote;
- Kung ang c ay infinity, walang mga pahalang na asymptotes.
Kung ang isang function ay isang ratio ng dalawang polynomial, kung gayon kung ang function ay may mga pahalang na asymptotes, hindi namin hahanapin ang mga pahilig na asymptotes - wala sila.
Tingnan natin ang mga halimbawa ng paghahanap ng mga asymptotes ng isang function:
Halimbawa 16.1. Hanapin ang mga asymptotes ng curve.
Solusyon X-1≠0; X≠1.
Tingnan natin kung tuwid ang linya x= 1 patayong asymptote. Upang gawin ito, kinakalkula namin ang limitasyon ng pag-andar sa punto x= 1: .
x= 1 - patayong asymptote.
Sa= .
Sa= = . kasi Sa=2 (numero), pagkatapos y=2– pahalang na asymptote.
Dahil ang isang function ay isang ratio ng mga polynomial, kung mayroong mga pahalang na asymptotes, iginiit namin na walang mga pahilig na asymptotes.
x= 1 at pahalang na asymptote y=2. Para sa kalinawan, ang graph ng function na ito ay ipinakita sa Fig. 16.2.
Halimbawa 16.2. Hanapin ang mga asymptotes ng curve.
Solusyon. 1. Hanapin ang domain ng kahulugan ng function: X-2≠0; X≠2.
Tingnan natin kung tuwid ang linya x= 2 patayong asymptote. Upang gawin ito, kinakalkula namin ang limitasyon ng pag-andar sa punto x= 2: .
Nakuha namin iyon, samakatuwid, x= 2 - patayong asymptote.
2. Upang maghanap ng mga pahalang na asymptotes, makikita namin ang: Sa= .
Dahil lumalabas ang kawalan ng katiyakan sa limitasyon, ginagamit namin ang panuntunan ng L'Hopital: Sa= = . kasi Sa– infinity, pagkatapos ay walang mga pahalang na asymptotes.
3. Upang maghanap ng mga oblique asymptotes, makikita namin ang:
Nakakuha kami ng isang kawalan ng katiyakan ng form , gamitin natin ang panuntunan ng L'Hopital: = =1. Kaya, 1. Hanapin natin b ayon sa formula: .
b= = =
Nakuha ko na b= 2. Pagkatapos y=kx+b – pahilig na asymptote. Sa aming kaso, ganito ang hitsura: y=x+2.
|
Mga tanong sa pagkontrol:
Lecture 17. PANGKALAHATANG SKEMA PARA SA PAG-AARAL NG FUNCTION AT PAGBUO NG GRAPH
Sa panayam na ito ay ibubuod natin ang lahat ng naunang pinag-aralan na materyal. Ang pangwakas na layunin ng aming mahabang paglalakbay ay ang masuri ang anumang ibinigay na function na ayon sa pagsusuri at bumuo ng graph nito. Ang mga mahahalagang bahagi ng aming pananaliksik ay ang pag-aaral ng function para sa extrema, ang pagtukoy ng mga pagitan ng monotonicity, convexity at concavity ng graph, ang paghahanap para sa mga inflection point at asymptotes ng graph ng function.
Isinasaalang-alang ang lahat ng mga aspeto sa itaas, ipinakita namin scheme para sa pag-aaral ng isang function at paglalagay ng graph .
1. Hanapin ang domain ng kahulugan ng function.
2. Suriin ang function para sa even-odd parity:
· kung , kung gayon ang function ay kahit na (ang graph ng isang even function ay simetriko tungkol sa axis OU);
· kung , kung gayon ang function ay kakaiba (ang graph ng isang kakaibang function ay simetriko na may kinalaman sa pinagmulan);
· kung hindi man ang function ay hindi kahit na o kakaiba.
3. Siyasatin ang function para sa periodicity (kabilang sa mga function na pinag-aaralan natin, ang trigonometric functions lang ang maaaring periodic).
4. Hanapin ang mga intersection point ng function graph na may mga coordinate axes:
· Oh: sa=0 (malutas lamang natin ang equation kung magagamit natin ang mga pamamaraang alam natin);
· OU: X=0.
5. Hanapin ang unang derivative ng function at mga kritikal na punto ng unang uri.
6. Maghanap ng monotonicity interval at extrema ng function.
7. Hanapin ang pangalawang derivative ng function at mga kritikal na punto ng pangalawang uri.
8. Hanapin ang mga pagitan ng convexity-concavity ng function graph at inflection point.
9. Hanapin ang mga asymptotes ng graph ng function.
10. Bumuo ng graph ng function. Kapag nagtatayo, dapat mong isaalang-alang mga kaso ng posibleng lokasyon ng graph malapit sa mga asymptotes :
11. Kung kinakailangan, pumili ng mga control point para sa mas tumpak na konstruksyon.
Isaalang-alang natin ang isang scheme para sa pag-aaral ng isang function at pagbuo ng graph nito gamit ang mga partikular na halimbawa:
Halimbawa 17.1. I-graph ang function.
Solusyon. 1. Ang function na ito ay tinukoy sa buong linya ng numero maliban sa X=3, kasi sa puntong ito ang denominator ay napupunta sa zero.
2. Upang matukoy kung ang isang function ay pantay o kakaiba, makikita natin ang:
Nakikita natin iyon at , samakatuwid, ay hindi isang kahit na o isang kakaibang function.
3. Ang function ay hindi pana-panahon.
4. Hanapin ang mga punto ng intersection sa mga coordinate axes. Upang mahanap ang punto ng intersection sa axis Oh tanggapin natin sa=0. Nakukuha namin ang equation: . Kaya, ang punto (0; 0) ay ang punto ng intersection sa mga coordinate axes.
5. Hanapin natin ang derivative ng function gamit ang rule of differentiation of fractions: = = = = .
Upang makahanap ng mga kritikal na punto, nakakahanap tayo ng mga punto kung saan ang derivative ng function ay katumbas ng 0 o wala.
Kung =0, samakatuwid . Ang produkto ay pagkatapos ay katumbas ng 0 kapag hindi bababa sa isa sa mga kadahilanan ay katumbas ng 0: o .
X-3) Ang 2 ay katumbas ng 0, ibig sabihin. ay hindi umiiral kapag X=3.
Kaya, ang function ay may tatlong kritikal na punto ng unang uri: ; ; .
6. Sa axis ng numero ay minarkahan namin ang mga kritikal na punto ng unang uri, at minarkahan namin ang punto ng isang punctured na tuldok, dahil ang function ay hindi tinukoy sa loob nito.
Inilalagay namin ang derivative = mga palatandaan sa bawat pagitan:
|
|
Sa mga pagitan kung saan , ang orihinal na function ay tumataas (sa (-∞;0]), kung saan - bumababa (sa ).
Dot X=0 ay ang pinakamataas na punto ng function. Upang mahanap ang maximum ng function, hanapin namin ang halaga ng function sa punto 0: .
Dot X=6 ay ang pinakamababang punto ng function. Upang mahanap ang minimum ng function, makikita namin ang halaga ng function sa punto 6: .
Ang mga resulta ng pananaliksik ay maaaring ilagay sa isang talahanayan. Ang bilang ng mga hilera sa talahanayan ay naayos at katumbas ng apat, at ang bilang ng mga hanay ay nakasalalay sa function na pinag-aaralan. Sa mga cell ng unang linya, ang mga agwat ay sunud-sunod na ipinasok kung saan hinahati ng mga kritikal na punto ang domain ng kahulugan ng function, kabilang ang mga kritikal na punto mismo. Upang maiwasan ang mga error kapag gumagawa ng mga punto na hindi kabilang sa domain ng kahulugan, hindi mo maaaring isama ang mga ito sa talahanayan.
Ang ikalawang linya ng talahanayan ay naglalaman ng mga senyales ng derivative sa bawat isa sa mga pagitan na isinasaalang-alang at ang halaga ng derivative sa mga kritikal na punto. Alinsunod sa mga palatandaan ng derivative ng function, ang mga pagitan ng pagtaas, pagbaba, at extrema ng function ay minarkahan sa ikatlong linya.
Ang huling linya ay nagsisilbing ipahiwatig ang maximum at minimum ng function.
| X | (-∞;0) | (0;3) | (3;6) | (6;+ ∞) | |||
| + | - | - | + | ||||
| f(x) | |||||||
| mga konklusyon | max | min |
7. Hanapin natin ang pangalawang derivative ng function bilang derivative ng unang derivative: = =
Ilagay natin sa numerator X-3 para sa mga bracket at gawin ang pagbabawas:
Ipakita natin ang mga katulad na termino sa numerator: .
Maghanap tayo ng mga kritikal na punto ng pangalawang uri: mga punto kung saan ang pangalawang derivative ng function ay katumbas ng zero o wala.
0 kung =0. Ang fraction na ito ay hindi maaaring katumbas ng zero, samakatuwid, walang mga punto kung saan ang pangalawang derivative ng function ay katumbas ng zero.
Wala kung denominator ( X-3) Ang 3 ay katumbas ng 0, i.e. ay hindi umiiral kapag X=3. :Oh , OU, pinanggalingan, mga yunit ng pagsukat para sa bawat axis.
Bago mag-plot ng isang function, kailangan mong:
Iguhit ang mga asymptotes na may mga tuldok na linya;
· markahan ang mga punto ng intersection sa mga coordinate axes;
|
· gamit ang nakuhang data sa mga pagitan ng pagtaas, pagbaba, convexity at concavity, bumuo ng isang graph ng function. Ang mga sangay ng graph ay dapat na "may posibilidad" sa mga asymptotes, ngunit hindi magsalubong sa kanila.
· suriin kung ang graph ng function ay tumutugma sa pananaliksik na isinagawa: kung ang function ay pantay o kakaiba, kung gayon kung ang symmetry ay sinusunod; Ang mga pagitan ba ng pagtaas at pagbaba, convexity at concavity, at inflection point ay tumutugma sa theoretically found ones?
11. Para sa mas tumpak na konstruksyon, maaari kang pumili ng ilang mga control point. Halimbawa, hanapin natin ang mga halaga ng function sa mga punto -2 at 7:
Inaayos namin ang iskedyul na isinasaalang-alang ang mga control point.
Mga tanong sa pagkontrol:
- Ano ang algorithm para sa pag-graph ng isang function?
- Maaari bang magkaroon ng extremum ang isang function sa mga punto sa labas ng domain ng kahulugan nito?
KABANATA 3. 3. INTEGRAL CALCULUS NG ISANG FUNCTION