Asimptotele graficului unei funcții
Fantoma asimptotei rătăcește pe site de mult timp pentru a se concretiza în sfârșit într-un articol separat și a aduce o încântare deosebită cititorilor care sunt nedumeriți studiul complet al funcției. Găsirea asimptotelor unui grafic este una dintre puținele părți ale acestei sarcini care este acoperită în cursul școlar doar într-o manieră de ansamblu, deoarece evenimentele gravitează în jurul calculului. limitele funcției, dar încă aparțin matematicii superioare. Pentru vizitatorii care înțeleg puțin analiza matematică, cred că indiciu este clar ;-) ...oprește-te, oprește-te, unde mergi? Limite- este ușor!
Exemple de asimptote au fost întâlnite imediat în prima lecție despre grafice ale funcţiilor elementare, iar subiectul primește acum o analiză detaliată.
Deci, ce este o asimptotă?
Imagina punct variabil, care „călătorește” de-a lungul graficului funcției. Asimptotul este Drept, la care aproape la nesfârşit graficul unei funcții se apropie pe măsură ce punctul ei variabil se deplasează la infinit.
Notă : Definiția este semnificativă, dacă aveți nevoie de o formulare în notație de calcul, vă rugăm să consultați manualul.
În plan, asimptotele sunt clasificate în funcție de locația lor naturală:
1) Asimptote verticale, care sunt date printr-o ecuație de forma , unde „alfa” este un număr real. Un reprezentant popular definește însăși axa ordonatelor,
cu o ușoară senzație de greață ne amintim de hiperbola.
2) Asimptote oblice scrisă în mod tradițional ecuația unei linii drepte cu un coeficient de unghi. Uneori, un caz special este identificat ca un grup separat - asimptote orizontale. De exemplu, aceeași hiperbolă cu asimptotă.
Să mergem repede, să atingem subiectul cu o scurtă explozie de mitralieră:
Câte asimptote poate avea graficul unei funcții?
Nici unul, unul, doi, trei,... sau la infinit. Nu vom merge departe pentru exemple, să ne amintim functii elementare. O parabolă, o parabolă cubică și o undă sinusoidală nu au deloc asimptote. Graficul unei funcții logaritmice exponențiale are o singură asimptotă. Arctangente și arccotangente au două dintre ele, iar tangenta și cotangente au infinit de multe. Nu este neobișnuit ca un grafic să aibă atât asimptote orizontale, cât și verticale. Hyperbole, te va iubi mereu.
Ce înseamnă ?
Asimptotele verticale ale graficului unei funcții
Asimptota verticală a graficului este de obicei localizată în punctul de discontinuitate infinită funcții. Este simplu: dacă într-un punct funcția suferă o discontinuitate infinită, atunci linia dreaptă specificată de ecuație este asimptota verticală a graficului.
Notă : Rețineți că intrarea este folosită pentru a se referi la două concepte complet diferite. Dacă un punct este implicit sau o ecuație a unei linii depinde de context.
Astfel, pentru a stabili prezența unei asimptote verticale într-un punct, este suficient să arătăm că cel puțin unul din limitele unilaterale 
infinit. Cel mai adesea acesta este punctul în care numitorul funcției este zero. În esență, am găsit deja asimptote verticale în ultimele exemple ale lecției asupra continuităţii unei funcţii. Dar, în unele cazuri, există o singură limită unilaterală, iar dacă este infinită, atunci din nou - iubiți și favorizați asimptota verticală. Cea mai simplă ilustrație: și axa ordonatelor (vezi. Grafice și proprietăți ale funcțiilor elementare).
Din cele de mai sus, rezultă și un fapt evident: dacă funcția este pornită continuă, atunci nu există asimptote verticale. Din anumite motive, mi-a venit în minte o parabolă. Într-adevăr, unde poți „lipi” o linie dreaptă aici? ...da... înțeleg... adepții unchiului Freud au devenit isterici =)
Afirmația inversă este în general falsă: de exemplu, funcția nu este definită pe întreaga linie numerică, ci este complet lipsită de asimptote.
Asimptote înclinate ale graficului unei funcții
Asimptotele oblice (ca caz special - orizontale) pot fi trase dacă argumentul funcției tinde spre „plus infinit” sau „minus infinit”. De aceea graficul unei funcții nu poate avea mai mult de două asimptote oblice. De exemplu, graficul unei funcții exponențiale are o singură asimptotă orizontală la , iar graficul arctangentei la are două astfel de asimptote și altele diferite.
Când graficul din ambele locuri se apropie de o singură asimptotă oblică, atunci „infiniturile” sunt de obicei combinate sub o singură intrare. De exemplu, ...ai ghicit corect: .
Regula generală de bază:
Dacă sunt două final limită 
, atunci linia dreaptă este asimptota oblică a graficului funcției la . Dacă cel puțin unul dintre limitele enumerate este infinită, atunci nu există nicio asimptotă oblică.
Notă : formulele rămân valabile dacă „x” tinde doar spre „plus infinit” sau doar către „minus infinit”.
Să arătăm că parabola nu are asimptote oblice: 
Limita este infinită, ceea ce înseamnă că nu există nicio asimptotă oblică. Rețineți că în găsirea limitei 
nevoia a dispărut deoarece răspunsul a fost deja primit.
Notă
: Dacă aveți (sau veți avea) dificultăți în înțelegerea semnelor plus-minus, minus-plus, vă rugăm să vedeți ajutorul de la începutul lecției
asupra funcţiilor infinitezimale, unde ți-am spus cum să interpretezi corect aceste semne.
Este evident că orice funcție pătratică, cubică, polinom de gradul 4 și superior nu are nici asimptote oblice.
Acum să ne asigurăm că și graficul nu are o asimptotă oblică. Pentru a dezvălui incertitudinea folosim Regula lui L'Hopital:
, care era ceea ce trebuia verificat.
Când funcția crește la infinit, dar nu există o linie dreaptă de care s-ar apropia graficul infinit de aproape.
Să trecem la partea practică a lecției:
Cum să găsiți asimptotele graficului unei funcții?
Exact așa este formulată sarcina tipică și implică găsirea TOATE asimptotele graficului (vertical, înclinat/orizontal). Deși, pentru a fi mai precis în a pune întrebarea, vorbim despre cercetarea prezenței asimptotelor (la urma urmei, s-ar putea să nu existe deloc). Să începem cu ceva simplu:
Exemplul 1
Găsiți asimptotele graficului unei funcții
Soluţie Este convenabil să o împărțim în două puncte:
1) Mai întâi verificăm dacă există asimptote verticale. Numitorul ajunge la zero la , și este imediat clar că în acest moment funcția are de suferit gol nesfârșit, iar linia dreaptă dată de ecuație este asimptota verticală a graficului funcției. Dar, înainte de a trage o astfel de concluzie, este necesar să se găsească limite unilaterale: 
Vă reamintesc de tehnica de calcul pe care m-am concentrat în mod similar în articol Continuitatea funcției. Puncte de pauză. În expresia de sub semnul limită înlocuim . Nu este nimic interesant la numărător:
.
Dar în numitor se dovedește număr negativ infinitezimal:
, determină soarta limitei.
Limita din stânga este infinită și, în principiu, este deja posibil să se pronunțe despre prezența unei asimptote verticale. Dar limitele unilaterale sunt necesare nu numai pentru asta, ci AJUTĂ LA ÎNȚELEGE CUM localizați graficul funcției și construiți-l CORECT. Prin urmare, trebuie să calculăm și limita pentru dreapta: 
Concluzie: limitele unilaterale sunt infinite, ceea ce înseamnă că linia dreaptă este asimptota verticală a graficului funcției la .
Prima limită finit, ceea ce înseamnă că este necesar să „continuați conversația” și să găsiți a doua limită:
Și a doua limită finit.
Astfel, asimptota noastră este:
Concluzie: dreapta dată de ecuație este asimptota orizontală a graficului funcției la .
Pentru a găsi asimptota orizontală
puteți folosi o formulă simplificată:
Daca exista finit limită, atunci linia dreaptă este asimptota orizontală a graficului funcției la .
Este ușor de observat că numărătorul și numitorul funcției aceeași ordine de creștere, ceea ce înseamnă că limita căutată va fi finită: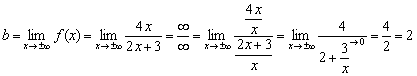 
Răspuns:
În funcție de condiție, nu trebuie să finalizați desenul, dar dacă este în plină desfășurare studiu de funcții, apoi pe schiță facem imediat o schiță: 
Pe baza celor trei limite găsite, încercați să vă dați seama singur cum ar putea fi localizat graficul funcției. Este deloc greu? Găsiți 5-6-7-8 puncte și marcați-le pe desen. Cu toate acestea, graficul acestei funcții este construit folosind transformări ale graficului unei funcţii elementare, iar cititorii care au examinat cu atenție Exemplul 21 al articolului de mai sus pot ghici cu ușurință ce fel de curbă este aceasta.
Exemplul 2
Găsiți asimptotele graficului unei funcții
Acesta este un exemplu de rezolvat singur. Permiteți-mi să vă reamintesc că este convenabil să împărțiți procesul în două puncte - asimptote verticale și asimptote oblice. În soluția eșantion, asimptota orizontală este găsită folosind o schemă simplificată.
În practică, funcțiile fracționale-raționale sunt cel mai des întâlnite, iar după antrenamentul pe hiperbole, vom complica sarcina:
Exemplul 3
Găsiți asimptotele graficului unei funcții 
Soluţie: Unu, doi și gata:
1) Sunt localizate asimptotele verticale în puncte de discontinuitate infinită, deci trebuie să verificați dacă numitorul ajunge la zero. Să decidem ecuație pătratică:
Discriminantul este pozitiv, deci ecuația are două rădăcini reale, iar munca este crescută semnificativ =) 
Pentru a găsi în continuare limite unilaterale, este convenabil să factorizezi trinomul pătrat:
(pentru notarea compactă, „minus” a fost inclus în prima paranteză). Pentru a fi în siguranță, haideți să verificăm prin deschiderea parantezelor mental sau la curent.
Să rescriem funcția în formă 
Să găsim limite unilaterale la punctul: 
Și la punctul: 
Astfel, liniile drepte sunt asimptote verticale ale graficului funcției în cauză.
2) Dacă te uiți la funcție 
, atunci este destul de evident că limita va fi finită și avem o asimptotă orizontală. Să-i arătăm prezența pe scurt: 
Astfel, linia dreaptă (axa absciselor) este asimptota orizontală a graficului acestei funcții.
Răspuns:
Limitele și asimptotele găsite oferă o mulțime de informații despre graficul funcției. Încercați să vă imaginați mental desenul ținând cont de următoarele fapte: 
Schițați versiunea dvs. a graficului pe schița dvs.
Desigur, limitele găsite nu determină clar aspectul graficului și este posibil să faceți o greșeală, dar exercițiul în sine vă va oferi un ajutor neprețuit în timpul studiu complet al funcției. Poza corectă este la sfârșitul lecției.
Exemplul 4
Găsiți asimptotele graficului unei funcții
Exemplul 5
Găsiți asimptotele graficului unei funcții 
Acestea sunt sarcini pentru soluții independente. Ambele grafice au din nou asimptote orizontale, care sunt detectate imediat de următoarele caracteristici: în Exemplul 4 ordinea de crestere numitor Mai mult, decât ordinea de creștere a numărătorului, iar în Exemplul 5 numărătorul și numitorul aceeași ordine de creștere. În soluția de probă, prima funcție este examinată pentru prezența asimptotelor oblice în totalitate, iar a doua - prin limită.
Asimptotele orizontale, în impresia mea subiectivă, sunt vizibil mai frecvente decât cele care sunt „cu adevărat înclinate”. Cazul general mult așteptat:
Exemplul 6
Găsiți asimptotele graficului unei funcții 
Soluţie: clasice ale genului:
1) Deoarece numitorul este pozitiv, atunci funcția continuu de-a lungul întregii linii numerice și nu există asimptote verticale. …Este bine? Nu este cuvântul potrivit - excelent! Punctul nr. 1 este închis.
2) Să verificăm prezența asimptotelor oblice:
Prima limită finit, deci să mergem mai departe. În timpul calculului a doua limită de eliminat incertitudine „infinit minus infinit” Aducem expresia la un numitor comun: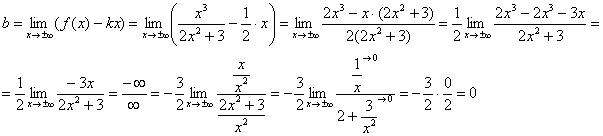 
Și a doua limită finit Prin urmare, graficul funcției în cauză are o asimptotă oblică:
Concluzie:
Astfel, când graficul funcției 
infinit de aproape se apropie de o linie dreaptă: 
Rețineți că își intersectează asimptota oblică la origine și astfel de puncte de intersecție sunt destul de acceptabile - este important ca „totul este normal” la infinit (de fapt, aici vorbim despre asimptote).
Exemplul 7
Găsiți asimptotele graficului unei funcții
Soluţie: Nu este nimic special de comentat, așa că voi elabora un exemplu aproximativ de soluție curată:
1) Asimptote verticale. Să explorăm ideea. 
Linia dreaptă este asimptota verticală pentru graficul de la .
2) Asimptote oblice: 
Linia dreaptă este asimptota înclinată pentru graficul de la .
Răspuns: 
Limitele și asimptotele unilaterale găsite ne permit să prezicem cu mare încredere cum arată graficul acestei funcții. Desenul corect la sfârșitul lecției.
Exemplul 8
Găsiți asimptotele graficului unei funcții
Acesta este un exemplu de soluție independentă; pentru comoditatea calculării unor limite, puteți împărți numărătorul la numitor termen cu termen. Din nou, atunci când analizați rezultatele, încercați să desenați un grafic al acestei funcții.
Evident, deținătorii de asimptote oblice „reale” sunt graficele acelor funcții raționale fracționale al căror cel mai înalt grad de numărător încă una cel mai înalt grad al numitorului. Dacă este mai mult, nu va exista nicio asimptotă oblică (de exemplu, ).
Dar alte miracole se întâmplă în viață:
Exemplul 9
Exemplul 11
Examinați graficul unei funcții pentru prezența asimptotelor
Soluţie: este evident că 
, prin urmare considerăm doar semiplanul drept, unde există un grafic al funcției.
Astfel, linia dreaptă (axa ordonatelor) este asimptota verticală pentru graficul funcției la .
2) Studiul asupra asimptotei oblice poate fi efectuat conform schemei complete, dar în articol Regulile lui L'Hopital am aflat că o funcție liniară are un ordin de creștere mai mare decât una logaritmică, prin urmare: 
(Vezi Exemplul 1 al aceleiași lecții).
Concluzie: axa x este asimptota orizontală a graficului funcției la .
Răspuns:
, Dacă ;
, Dacă .
Desen pentru claritate: 
Este interesant că o funcție aparent similară nu are deloc asimptote (cei care doresc pot verifica acest lucru).
Două exemple finale pentru auto-studiu:
Exemplul 12
Examinați graficul unei funcții pentru prezența asimptotelor 
Asimptota graficului unei funcții y = f(x) este o linie dreaptă care are proprietatea că distanța de la punctul (x, f(x)) până la această linie dreaptă tinde spre zero pe măsură ce punctul grafic se deplasează nedefinit de la origine.
În figura 3.10. sunt date exemple grafice vertical, orizontalăȘi înclinat asimptotă.
Găsirea asimptotelor graficului se bazează pe următoarele trei teoreme.
Teorema asimptotei verticale. Fie definită funcția y = f(x) într-o anumită vecinătate a punctului x 0 (eventual excluzând acest punct în sine) și cel puțin una dintre limitele unilaterale ale funcției este egală cu infinitul, i.e. Atunci linia dreaptă x = x 0 este asimptota verticală a graficului funcției y = f(x).
Evident, linia dreaptă x = x 0 nu poate fi o asimptotă verticală dacă funcția este continuă în punctul x 0, deoarece în acest caz 
. În consecință, asimptotele verticale ar trebui căutate în punctele de discontinuitate ale funcției sau la capetele domeniului său de definire.
Teorema asimptotei orizontale. Fie definită funcția y = f(x) pentru x suficient de mare și există o limită finită a funcției. Atunci linia y = b este asimptota orizontală a graficului funcției.
Cometariu. Dacă numai una dintre limite este finită, atunci funcția are, în consecință, stângaci sau pe partea dreaptă asimptotă orizontală.
În cazul în care , funcția poate avea o asimptotă oblică.
Teorema asimptotei oblice. Fie definită funcția y = f(x) pentru x suficient de mare și există limite finite 
. Atunci linia dreaptă y = kx + b este asimptota înclinată a graficului funcției.
Nicio dovadă.
O asimptotă oblică, la fel ca una orizontală, poate fi dreaptă sau stângă dacă baza limitelor corespunzătoare este infinitatea unui anumit semn.
Studierea funcțiilor și construirea graficelor acestora include de obicei următorii pași:
1. Găsiți domeniul de definire al funcției.
2. Examinați funcția pentru paritatea par-impar.
3. Găsiți asimptote verticale examinând punctele de discontinuitate și comportamentul funcției la limitele domeniului de definiție, dacă acestea sunt finite.
4. Găsiți asimptote orizontale sau oblice examinând comportamentul funcției la infinit.
5. Găsiți extremele și intervalele de monotonitate ale funcției.
6. Aflați intervalele de convexitate ale funcției și punctele de inflexiune.
7. Aflați punctele de intersecție cu axele de coordonate și, eventual, câteva puncte suplimentare care clarifică graficul.
Diferenţial de funcţie
Se poate dovedi că dacă o funcție are o limită egală cu un număr finit pentru o anumită bază, atunci ea poate fi reprezentată ca sumă a acestui număr și o valoare infinitezimală pentru aceeași bază (și invers): .
Sa aplicam aceasta teorema unei functii diferentiabile: .
Astfel, incrementul funcției Dу este format din doi termeni: 1) liniar față de Dx, adică. f `(x)Dх; 2) neliniar în raport cu Dx, i.e. a(Dx)Dх. În același timp, de când 
, acest al doilea termen este un infinitezimal de ordin mai mare decât Dx (cum Dx tinde spre zero, tinde spre zero și mai repede).
Diferenţial funcția este partea principală, liniară relativă la Dx a incrementului funcției, egală cu produsul derivatei și incrementul variabilei independente dy = f `(x)Dx.
Să găsim diferența funcției y = x.
Deoarece dy = f `(x)Dх = x`Dх = Dх, atunci dx = Dх, i.e. diferenţialul unei variabile independente este egal cu incrementul acestei variabile.
Prin urmare, formula pentru diferența unei funcții poate fi scrisă ca dy = f `(x)dх. De aceea, una dintre notațiile pentru derivată este fracția dy/dx.
Se ilustrează semnificația geometrică a diferenţialului
Figura 3.11. Să luăm un punct arbitrar M(x, y) pe graficul funcției y = f(x). Să dăm argumentului x incrementul Dx. Atunci funcția y = f(x) va primi incrementul Dy = f(x + Dx) - f(x). Să desenăm o tangentă la graficul funcției în punctul M, care formează un unghi a cu direcția pozitivă a axei absciselor, adică. f `(x) = tan a. Din triunghiul dreptunghic MKN
KN = MN*tg a = Dх*tg a = f `(x)Dх = dy.
Astfel, diferența unei funcții este incrementul în ordonată a tangentei trasate la graficul funcției într-un punct dat când x primește incrementul Dx.
Proprietățile unei diferențiale sunt practic aceleași cu cele ale unei derivate:
3. d(u ± v) = du ± dv.
4. d(uv) = v du + u dv.
5. d(u/v) = (v du - u dv)/v 2.
Cu toate acestea, există o proprietate importantă a diferenţialului unei funcţii pe care derivata ei nu o are - aceasta este invarianta formei diferentiale.
Din definirea diferenţialului pentru funcţia y = f(x), diferenţialul dy = f `(x)dх. Dacă această funcție y este complexă, i.e. y = f(u), unde u = j(x), atunci y = f și f `(x) = f `(u)*u`. Atunci dy = f `(u)*u`dх. Dar pentru funcție
u = j(x) diferential du = u`dх. Prin urmare dy = f `(u)*du.
Comparând egalitățile dy = f`(x)dх și dy = f`(u)*du, ne asigurăm că formula diferențială nu se schimbă dacă în loc de o funcție a variabilei independente x considerăm o funcție a variabila dependenta u. Această proprietate a diferenţialului se numeşte invarianţă (adică imuabilitate) a formei (sau formulei) diferenţialului.
Cu toate acestea, există încă o diferență între aceste două formule: în prima dintre ele, diferența variabilei independente este egală cu incrementul acestei variabile, i.e. dx = Dx, iar în al doilea rând, diferența funcției du este doar partea liniară a incrementului acestei funcție Du și numai pentru Dx mic du » Du.
Soluția poate fi împărțită convenabil în două puncte:
1) Mai întâi verificăm dacă există asimptote verticale. Numitorul ajunge la zero la, și este imediat clar că în acest punct funcția suferă o discontinuitate infinită, iar linia dreaptă specificată de ecuație este asimptota verticală a graficului funcției. Dar, înainte de a trage o astfel de concluzie, este necesar să se găsească limite unilaterale:
Vă reamintesc de tehnica de calcul pe care m-am concentrat în mod similar în articolul Continuitatea unei funcții. Puncte de rupere. Înlocuim „X” în expresia de sub semnul limită. Nu este nimic interesant la numărător:
Dar numitorul are ca rezultat un număr negativ infinitezimal:
Ea determină soarta limitei.
Limita din stânga este infinită și, în principiu, este deja posibil să se pronunțe despre prezența unei asimptote verticale. Dar limitele unilaterale sunt necesare nu numai pentru aceasta, ci AJUTĂ LA ÎNȚELEGEREA CUM este situat graficul unei funcții și la construirea CORECT. Prin urmare, trebuie să calculăm și limita pentru dreapta:
Concluzie: limitele unilaterale sunt infinite, ceea ce înseamnă că linia dreaptă este asimptota verticală a graficului funcției la.
Prima limită este finită, ceea ce înseamnă că trebuie să „continuăm conversația” și să găsim a doua limită:
A doua limită este, de asemenea, finită.
Astfel, asimptota noastră este:
Concluzie: linia dreaptă specificată de ecuație este asimptota orizontală a graficului funcției at.
Pentru a găsi asimptota orizontală, puteți utiliza o formulă simplificată:
Dacă există o limită finită, atunci linia dreaptă este asimptota orizontală a graficului funcției la.
Este ușor de observat că numărătorul și numitorul funcției sunt de aceeași ordine de creștere, ceea ce înseamnă că limita căutată va fi finită:
În funcție de condiție, nu este nevoie să facem un desen, dar dacă ne aflăm în mijlocul cercetării unei funcții, atunci facem imediat o schiță asupra schiței:
Pe baza celor trei limite găsite, încercați să vă dați seama singur cum ar putea fi localizat graficul funcției. Este deloc greu? Găsiți 5-6-7-8 puncte și marcați-le pe desen. Cu toate acestea, graficul acestei funcții este construit folosind transformări ale graficului unei funcții elementare, iar cititorii care au examinat cu atenție Exemplul 21 al acestui articol pot ghici cu ușurință ce fel de curbă este aceasta.
Acesta este un exemplu de rezolvat singur. Permiteți-mi să vă reamintesc că procesul este împărțit convenabil în două puncte - asimptote verticale și asimptote oblice. În soluția eșantion, asimptota orizontală este găsită folosind o schemă simplificată.
În practică, funcțiile fracționale-raționale sunt cel mai des întâlnite, iar după antrenamentul pe hiperbole, vom complica sarcina:
Găsiți asimptotele graficului unei funcții
Soluție: unu, doi și gata:
1) Asimptotele verticale sunt în puncte de discontinuitate infinită, așa că trebuie să verificați dacă numitorul ajunge la zero. Să rezolvăm ecuația pătratică:
Discriminantul este pozitiv, deci ecuația are două rădăcini reale, iar munca se adaugă semnificativ
Pentru a găsi în continuare limite unilaterale, este convenabil să factorizezi trinomul pătrat:
(pentru notarea compactă, „minus” a fost inclus în prima paranteză). Pentru a fi în siguranță, haideți să verificăm prin deschiderea parantezelor mental sau la curent.
Să rescriem funcția în formă
Să găsim limite unilaterale la punctul:
limita funcției graficului asimptot
Și la punctul:
Astfel, liniile drepte sunt asimptote verticale ale graficului funcției în cauză.
2) Dacă te uiți la funcție, este destul de evident că limita va fi finită și avem o asimptotă orizontală. Să-i arătăm prezența pe scurt:
Astfel, linia dreaptă (axa absciselor) este asimptota orizontală a graficului acestei funcții.
Limitele și asimptotele găsite oferă o mulțime de informații despre graficul funcției. Încercați să vă imaginați mental desenul ținând cont de următoarele fapte:
Schițați versiunea dvs. a graficului pe schița dvs.
Desigur, limitele găsite nu determină în mod clar aspectul graficului și este posibil să faceți o greșeală, dar exercițiul în sine va oferi o asistență neprețuită în cursul unui studiu complet al funcției. Poza corectă este la sfârșitul lecției.
Găsiți asimptotele graficului unei funcții
Găsiți asimptotele graficului unei funcții
Acestea sunt sarcini pentru soluții independente. Ambele grafice au din nou asimptote orizontale, care sunt detectate imediat de următoarele caracteristici: în exemplul 4, ordinea de creștere a numitorului este mai mare decât ordinea de creștere a numărătorului, iar în exemplul 5, numărătorul și numitorul sunt de aceeași ordine de creștere. În soluția de probă, prima funcție este examinată pentru prezența asimptotelor oblice în întregime, iar a doua - prin limită.
Asimptotele orizontale, în impresia mea subiectivă, sunt vizibil mai frecvente decât cele care sunt „cu adevărat înclinate”. Cazul general mult așteptat:
Găsiți asimptotele graficului unei funcții
Soluție: clasic al genului:
- 1) Deoarece numitorul este pozitiv, funcția este continuă de-a lungul întregii drepte numerice și nu există asimptote verticale. …Este bine? Nu este cuvântul potrivit - excelent! Punctul nr. 1 este închis.
- 2) Să verificăm prezența asimptotelor oblice:
A doua limită este, de asemenea, finită, prin urmare, graficul funcției în cauză are o asimptotă oblică:
Astfel, atunci când graficul funcției se apropie de o dreaptă infinit apropiată.
Rețineți că își intersectează asimptota oblică la origine și astfel de puncte de intersecție sunt destul de acceptabile - este important ca „totul este normal” la infinit (de fapt, aici vorbim despre asimptote).
Găsiți asimptotele graficului unei funcții
Soluție: nu este nimic special de comentat, așa că voi întocmi un exemplu aproximativ de soluție finală:
1) Asimptote verticale. Să explorăm ideea.
Linia dreaptă este asimptota verticală pentru graficul la.
2) Asimptote oblice:
Linia dreaptă este asimptota înclinată pentru graficul la.
Limitele și asimptotele unilaterale găsite ne permit să prezicem cu mare încredere cum arată graficul acestei funcții.
Găsiți asimptotele graficului unei funcții
Acesta este un exemplu de soluție independentă; pentru comoditatea calculării unor limite, puteți împărți numărătorul la numitor termen cu termen. Din nou, atunci când analizați rezultatele, încercați să desenați un grafic al acestei funcții.
Evident, deținătorii de asimptote oblice „reale” sunt graficele acelor funcții raționale fracționale în care gradul de conducere al numărătorului este cu unul mai mare decât gradul de conducere al numitorului. Dacă este mai mult, nu va mai exista o asimptotă oblică (de exemplu).
Dar alte miracole se întâmplă în viață.
- Conceptul de asimptote
Una dintre etapele importante ale construirii graficelor de funcții este căutarea asimptotelor. Am întâlnit asimptote de mai multe ori: atunci când construim grafice de funcții, y=tgx, y=сtgx. Le-am definit drept linii pe care graficul unei funcții „tinde”, dar nu le traversează niciodată. A sosit momentul să oferim o definiție precisă a asimptotelor.
Există trei tipuri de asimptote: verticale, orizontale și oblice. În desen, asimptotele sunt de obicei notate prin linii punctate.
Să luăm în considerare următorul grafic al funcției construit artificial (Fig. 16.1), al cărui exemplu arată toate tipurile de asimptote:
Să definim fiecare tip de asimptotă:
1. Direct x=a numit asimptotă verticală funcții dacă .
2. Direct y=c numit asimptotă orizontală funcții dacă .
3. Direct y=kx+b numit asimptotă oblică funcții dacă .
Geometric, definiția unei asimptote oblice înseamnă că la →∞ graficul funcției se apropie de o dreaptă cât se dorește y=kx+b, adică sunt aproape identice. Diferența dintre expresii practic identice tinde spre zero.
Rețineți că asimptotele orizontale și oblice sunt considerate numai în condiția →∞. Uneori ele se disting în asimptote orizontale și oblice la →+∞ și →-∞.
- Algoritm pentru căutarea asimptotelor
Pentru a găsi asimptote, puteți utiliza următorul algoritm:
Pot exista una, mai multe sau nicio asimptotă verticală.
- Dacă c este un număr, atunci y=c– asimptotă orizontală;
- Dacă c este infinit, atunci nu există asimptote orizontale.
Dacă o funcție este un raport de două polinoame, atunci dacă funcția are asimptote orizontale, nu vom căuta asimptote oblice - acestea nu există.
Să ne uităm la exemple de găsire a asimptotelor unei funcții:
Exemplul 16.1. Găsiți asimptotele curbei.
Soluţie X-1≠0; X≠1.
Să verificăm dacă linia este dreaptă x= 1 asimptotă verticală. Pentru a face acest lucru, calculăm limita funcției în punct x= 1: .
x= 1 - asimptotă verticală.
Cu= .
Cu= = . Deoarece Cu=2 (număr), atunci y=2– asimptotă orizontală.
Deoarece o funcție este un raport de polinoame, dacă există asimptote orizontale, afirmăm că nu există asimptote oblice.
x= 1 și asimptotă orizontală y=2. Pentru claritate, graficul acestei funcții este prezentat în Fig. 16.2.
Exemplul 16.2. Găsiți asimptotele curbei.
Soluţie. 1. Găsiți domeniul de definire al funcției: X-2≠0; X≠2.
Să verificăm dacă linia este dreaptă x= 2 asimptote verticale. Pentru a face acest lucru, calculăm limita funcției în punct x= 2: .
Prin urmare, am înțeles că x= 2 - asimptotă verticală.
2. Pentru a căuta asimptote orizontale, găsim: Cu= .
Deoarece incertitudinea apare în limită, folosim regula lui L'Hopital: Cu= = . Deoarece Cu– infinit, atunci nu există asimptote orizontale.
3. Pentru a căuta asimptote oblice, găsim:
Am obținut o incertitudine de forma , să folosim regula lui L'Hopital: = =1. Deci, 1. Să găsim b dupa formula: .
b= = =
Am inteles b= 2. Apoi y=kx+b – asimptotă oblică. In cazul nostru arata asa: y=x+2.
|
Întrebări de control:
Cursul 17. SCHEMA GENERALĂ DE STUDIAREA O FUNCȚIE ȘI CONSTRUIREA UNUI GRAF
În această prelegere vom rezuma tot materialul studiat anterior. Scopul final al călătoriei noastre lungi este să putem examina orice funcție dată analitic și să construim graficul acesteia. Părți importante ale cercetării noastre vor fi studiul funcției pentru extrema, determinarea intervalelor de monotonitate, convexitate și concavitate a graficului, căutarea punctelor de inflexiune și asimptote ale graficului funcției.
Ținând cont de toate aspectele de mai sus, vă prezentăm schema de studiere a unei functii si trasarea unui grafic .
1. Găsiți domeniul de definire al funcției.
2. Examinați funcția pentru paritatea par-impar:
· dacă , atunci funcția este pară (graficul unei funcții pare este simetric în raport cu axa OU);
· dacă , atunci funcția este impară (graficul unei funcții impare este simetric față de origine);
· în caz contrar, funcția nu este nici pară, nici impară.
3. Investigați funcția pentru periodicitate (dintre funcțiile pe care le studiem, numai funcțiile trigonometrice pot fi periodice).
4. Găsiți punctele de intersecție ale graficului funcției cu axele de coordonate:
· Oh: la=0 (rezolvăm ecuația doar dacă putem folosi metode cunoscute nouă);
· OU: X=0.
5. Aflați derivata întâi a funcției și punctele critice de primul fel.
6. Găsiți intervalele de monotonitate și extremele funcției.
7. Aflați derivata a doua a funcției și punctele critice de al doilea fel.
8. Aflați intervalele de convexitate-concavitate ale graficului funcției și punctele de inflexiune.
9. Aflați asimptotele graficului funcției.
10. Construiți un grafic al funcției. Când construiți, ar trebui să luați în considerare cazuri de posibilă localizare a graficului lângă asimptote :
11. Dacă este necesar, selectați punctele de control pentru o construcție mai precisă.
Să luăm în considerare o schemă pentru studierea unei funcții și construirea graficului acesteia folosind exemple specifice:
Exemplul 17.1. Reprezentați grafic funcția.
Soluţie. 1. Această funcție este definită pe întreaga linie numerică, cu excepția X=3, pentru că în acest moment numitorul ajunge la zero.
2. Pentru a determina dacă o funcție este pară sau impară, găsim:
Vedem că și , prin urmare, nu este nici o funcție pară, nici impară.
3. Funcția este neperiodică.
4. Aflați punctele de intersecție cu axele de coordonate. Pentru a găsi punctul de intersecție cu axa Oh hai sa acceptam la=0. Obținem ecuația: . Deci, punctul (0; 0) este punctul de intersecție cu axele de coordonate.
5. Să găsim derivata funcției folosind regula de diferențiere a fracțiilor: = = = = .
Pentru a găsi puncte critice, găsim puncte la care derivata funcției este egală cu 0 sau nu există.
Dacă =0, deci . Produsul este atunci egal cu 0 când cel puțin unul dintre factori este egal cu 0: sau .
X-3) 2 este egal cu 0, i.e. nu există când X=3.
Deci, funcția are trei puncte critice de primul fel: ; ; .
6. Pe axa numerelor se marchează puncte critice de primul fel, iar punctul se marchează cu un punct perforat, deoarece funcția nu este definită în ea.
Punem derivata = semnele pe fiecare interval:
|
|
La intervalele în care , funcția inițială crește (la (-∞;0]), unde - descrește (la ).
Punct X=0 este punctul maxim al funcției. Pentru a găsi maximul funcției, găsim valoarea funcției în punctul 0: .
Punct X=6 este punctul minim al funcției. Pentru a găsi minimul funcției, găsim valoarea funcției la punctul 6: .
Rezultatele cercetării pot fi introduse într-un tabel. Numărul de rânduri din tabel este fix și egal cu patru, iar numărul de coloane depinde de funcția studiată. În celulele primei linii sunt introduse secvenţial intervale în care punctele critice împart domeniul de definire a funcţiei, inclusiv punctele critice în sine. Pentru a evita erorile la construirea punctelor care nu aparțin domeniului definiției, nu le puteți include în tabel.
A doua linie a tabelului conține semnele derivatei pe fiecare dintre intervalele luate în considerare și valoarea derivatei în punctele critice. În conformitate cu semnele derivatei funcției, intervalele de creștere, scădere și extreme ale funcției sunt marcate pe a treia linie.
Ultima linie servește la indicarea maximului și minimului funcției.
| X | (-∞;0) | (0;3) | (3;6) | (6;+ ∞) | |||
| + | - | - | + | ||||
| f(x) | |||||||
| concluzii | max | min |
7. Să găsim derivata a doua a funcției ca și derivata primei derivate: = =
Să-l punem la numărător X-3 pentru paranteze și efectuați reducerea:
Să prezentăm termeni similari la numărător: .
Să găsim puncte critice de al doilea fel: puncte la care derivata a doua a funcției este egală cu zero sau nu există.
0 dacă =0. Această fracție nu poate fi egală cu zero, prin urmare, nu există puncte în care derivata a doua a funcției să fie egală cu zero.
Nu există dacă numitorul ( X-3) 3 este egal cu 0, i.e. nu există când X=3. :Oh, OU, origine, unități de măsură pentru fiecare axă.
Înainte de a trasa o funcție, trebuie să:
Desenați asimptotele cu linii punctate;
· marcați punctele de intersecție cu axele de coordonate;
|
· folosind datele obținute privind intervalele de creștere, scădere, convexitate și concavitate, construiți un grafic al funcției. Ramurile graficului ar trebui să „tindă” spre asimptote, dar nu să le intersecteze.
· verifica dacă graficul funcţiei corespunde cercetării efectuate: dacă funcţia este pară sau impară, atunci dacă se respectă simetria; Intervalele de creștere și scădere, convexitate și concavitate și punctele de inflexiune corespund celor găsite teoretic?
11. Pentru o construcție mai precisă, puteți selecta mai multe puncte de control. De exemplu, să găsim valorile funcției la punctele -2 și 7:
Ajustăm programul ținând cont de punctele de control.
Întrebări de control:
- Care este algoritmul pentru reprezentarea grafică a unei funcții?
- Poate o funcție să aibă un extremum în puncte în afara domeniului său de definiție?
CAPITOLUL 3. 3. CALCULUL INTEGRAL AL O FUNCȚIE